Volume Formulas

Prisms

The volume of a prism can be found by multiplying the base area of the prism $A$ by the height of the prism $h$. The prism itself may be slanted without any change to the volume formula, but the measurement of $h$ must be done perpendicular to the base. A cylinder is just a special type of prism with a circle as the base (in this case $A=\pi r^2$). A slanted rectangular prism is called a parallelepiped.

Volume of a prism

$$\boxed{V=Ah}$$

The height $h$ must be measured perpendicular to the base of area $A$ in order for this formula to be valid.

Yes, both of the figures above indeed have the same volume given by the same formula $V=Ah$. This initially puzzling fact regarding equal volumes has gained enough notoriety among mathematicians to warrant its own name: Cavalieri’s principle.

Some teachers provide more specific formulas that stem from this general principle. Some examples are below, but the only one that you technically need to commit to memory is the boxed equation above.

Formula	Figure
$V=s^{2}h$	Prism with square base of side length $s$ and height $h$.
$V=s^3$	Cube with side length $s$ and height $h$.
$V=lwh$	Prism with rectangular base of length $l$, width $w$, and height $h$
$V=\pi r^{2}h$	Cylinder of radius $r$ and height $h.$ (Prism with circular base of radius $r$.)

Pyramids

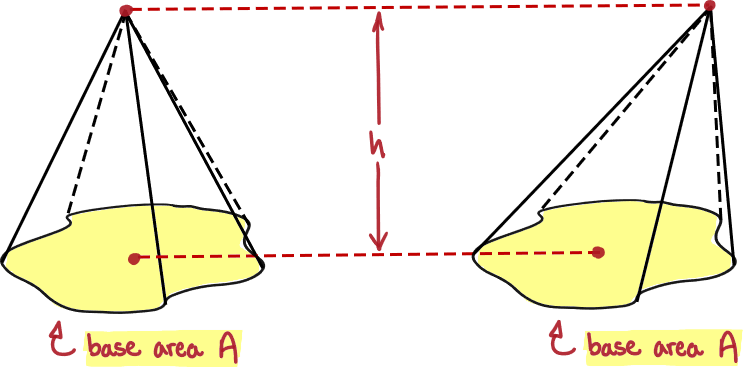
The volume of a pyramid can be found by computing one third of the product of the base area of the prism $A$ by the height of the prism $h$. The pyramid itself may be slanted without any change to the volume formula, but the measurement of $h$ must be done perpendicular to the base. A cone is just a special type of pyramid with a circle as the base (in this case $A=\pi r^2$).

Volume of a pyramid

$$\boxed{V=\frac{1}{3}Ah}$$

The height $h$ must be measured perpendicular to the base of area $A$ in order for this formula to be valid.

Students who have completed their first calculus course should be able to derive this formula by performing an appropriate volume of revolution integral.

Some teachers provide more specific formulas that stem from this general principle. Some examples are below, but the only one that you technically need to commit to memory is the boxed equation above.

Formula	Figure
$V=\frac{1}{3}{s}^{2}h$	Pyramid with square base of side length $s$ and height $h$.
$V=\frac{1}{3}lwh$	Pyramid with rectangular base of length $l$ and width $w$.
$V=\frac{1}{3}\pi r^{2}h$	Cone of radius $r$. (Pyramid with circular base of radius $r$.)

Spheres

The volume of a sphere with radius $r$ is given by the formula below.

Volume of a sphere

$$V=\frac{4}{3}\pi r^3$$

Students who have completed their first calculus course should be able to derive this formula by performing an appropriate volume of revolution integral.