Work (Energy Transfer) via Integrals

Definition of Work

The work $W$ done by a constant force $\vec{F}$ acting on an object as it undergoes displacement $\Delta \vec{x}$ is defined by

$$W=\vec{F}\cdot \Delta \vec{x}.$$

Conceptually, the work $W$ represents a transfer of energy into or out of the object in question. When $W>0,$ energy is being transferred into the object and when $W<0,$ energy is removed from the object.

The most common sets of units of measure for Work (energy), Force, and Displacement compatible with this equation are as follows.

System	Force	Displacement	Work (Energy)
SI/Metric	Newtons (N)	meters (m)	Joules (J)
Imperial	pounds (lb)	inches (in)	inch-pounds (in-lb)
Imperial	pounds (lb)	feet (ft)	foot-pounds (ft-lb)

The constant-force definition above works well for simple situations, but may need to be turned into an integral. A common general situation involving position-dependent forces is shown below.

Position-Dependent Forces

Imagine an object moving along the $x$ axis under the influence of a force $F(x)$ (also oriented along the $x$ axis) that varies as a function of the object’s position $x$. The work can be approximated by splitting up the path at various points $x_i$ along the path, computing the work $W_i=F(x_i)\Delta x$ at each point, and summing up the values.

$$W\approx \sum W_i=\sum F(x_i)\Delta x$$

Taking the limit as $\Delta x\to 0$ turns the summation into an integral, which provides the exact work done along the path.

$$\begin{array}{c}W=\underset{\Delta x\to 0}{\lim }\sum F(x_i)\Delta x\\ \boxed{W={\int }_{x_1}^{x_2}F(x)dx}\end{array}$$

Here, in this integral, $x_1$ and $x_2$ represent the initial and final $x$ positions of the object along its path.

Problems

Problems are taken from Calculus 10th ed. by Larson, Section 7.5 (Work)

Question 9

Seven and one-half foot-pounds of work is required to compress a spring $2$ inches from its natural length. Find the work required to compress the spring an additional one-half inch.

Note: this problem requires Hooke’s law, which says that the force exerted by a string $F,$ the stiffness of the spring $k$ (spring constant), and the distance the spring is stretched/squished from equilibrium $d$ are related by $F=kd.$

Solution 9

Let $x$ be the degree of compression of the spring at any given moment. According to Hooke’s law, the corresponding force would be of strength $F=kx,$ where $k$ is the stiffness (spring constant) of the spring.

We can equivalently view $x$ as the position of the tip of the spring that we are exerting the force to in order to compress it. Hence, we are dealing with a position-dependent force $F(x)=kx$, from which we can use the integral described earlier on this page to compute the work.

$$W={\int }_{x_1}^{x_2}Fdx={\int }_{x_1}^{x_2}kxdx$$

First, let’s equate the work done when moving the end of the spring from $x_1=0\text{ft}$ to $x_2=2\text{ in}=\frac{1}{6}\text{ft}$ with $7.5\text{ft}\cdot \text{lb}$ in order to determine the stiffness of the spring $k.$

$$\begin{array}{c}7.5\text{ft}\cdot \text{lb}={\int }_{0\text{in}}^{\frac{1}{6}\text{ft}}kxdx\\ 7.5\text{ft}\cdot \text{lb}={\frac{1}{2}k{x}^2|}_{0\text{in}}^{\frac{1}{6}\text{ft}}\\ 7.5\cancel{\text{ft}}\cdot \text{lb}=\frac{k}{72}{\text{ft}}^{\cancel{2}}\\ k=\frac{5}{48}\frac{\text{lb}}{\text{ft}}\end{array}$$

Now, use this value of $k$ to compute the work done from $x_1=0\text{ft}$ to $x=2.5\text{in}=\frac{5}{24}\text{ft}$.

$$\begin{array}{c}W={\int }_{0\text{ft}}^{\frac{5}{24}\text{ft}}\left(\frac{5}{48}\frac{\text{lb}}{\text{ft}}\right)xdx\\ W={\frac{5}{96}{x}^2|}_{0\text{ft}}^{\frac{5}{24}\text{ft}}\\ W=\frac{125}{55296}\text{ft-lb}\approx \boxed{0.002\text{ft-lb}}\end{array}$$

Question 19

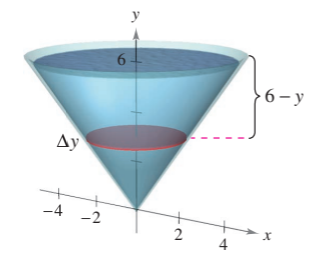
An open tank has the shape of a right circular cone (see figure). The tank is 8 feet across the top and $6$ feet high. How much work is done in emptying the tank by pumping the water over the top edge?

Note: the density of water is $62.4\frac{\text{lb}}{{\text{ft}}^3}$.

Solution 19

In the diagram, a cylindrical slice of water of thickness $\Delta y$ is highlighted. The volume of this slice of water is

$$\Delta V=\pi r^2\Delta y$$

where $r$ is the radius of the circular top and bottom of the cylinder.

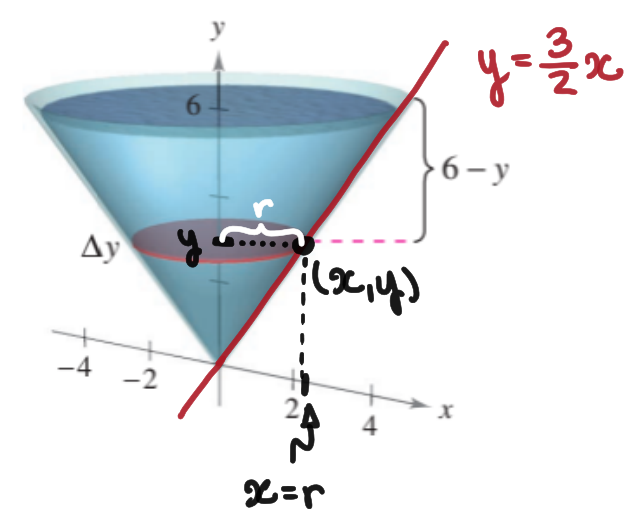
The lateral surface of the cone intersects the first quadrant of the $xy$ plane by means of a straight line of slope $\frac{3}{2}$ that intersects the origin, which has equation $y=\frac{3}{2}x$. The values of $r$ are given by the $x$ coordinates of points on this line for any value of $y$ within the cone, as illustrated below.

Hence, the radius of the circle is given as a function of $y$ by

$$r=\frac{2}{3}y$$

which gives the volume

$$\Delta V=\frac{4\pi y^2}{9}\Delta y.$$

The small amount of force $\Delta F$ required to lift this slice of water is given by multiplying this volume by the density of the water. This itself a function of $y$, the $y$-coordinate of the water slice, so below I will write $\Delta F(y)$.

$$\Delta F(y)=62.4\frac{\text{lb}}{{\text{ft}}^3}\cdot \Delta V=62.4\frac{\text{lb}}{{\text{ft}}^3}\cdot \frac{4\pi y^2}{9}\Delta y$$

Each slice needs to be lifted up by a height of $6-y$ in order to be poured over the top edge, which corresponds to a work of $\Delta F(y)(6-y)$. Summing up these works for various slices at $y$ coordinates $y_i$ from $y=0\text{ft}$ to $y=6\text{ft}$ allows us to approximate the total work needed.

$$\begin{array}{c}W\approx \sum \Delta F(y_i)(6-y_i)\\ W\approx \sum 62.4\cdot \frac{4\pi y_i^2}{9}\Delta y\cdot (6-y_i)\end{array}$$

Taking the limit as $\Delta y\to 0$ turns this into an integral and also yields the exact value for $W.$

$$\begin{array}{c}W=\underset{\Delta y\to 0}{\lim }\sum 62.4\cdot \frac{4\pi y^2}{9}\Delta y\cdot (6-y)\\ W={\int }_{0\text{ft}}^{6\text{ft}}62.4\cdot \frac{4\pi y^2}{9}dy\cdot (6-y)\\ W=62.4\cdot \frac{4\pi }{9}{\int }_0^{6}6y^2-y^{3}dy\\ W={62.4\cdot \frac{4\pi }{9}\left(2y^3-\frac{1}{4}{y}^4\right)|}_0^{6}6y^2\\ W=\frac{14976\pi }{5}\approx \boxed{9409.698\text{ft-lb}}\end{array}$$