SAT Important Formulas

Permalink

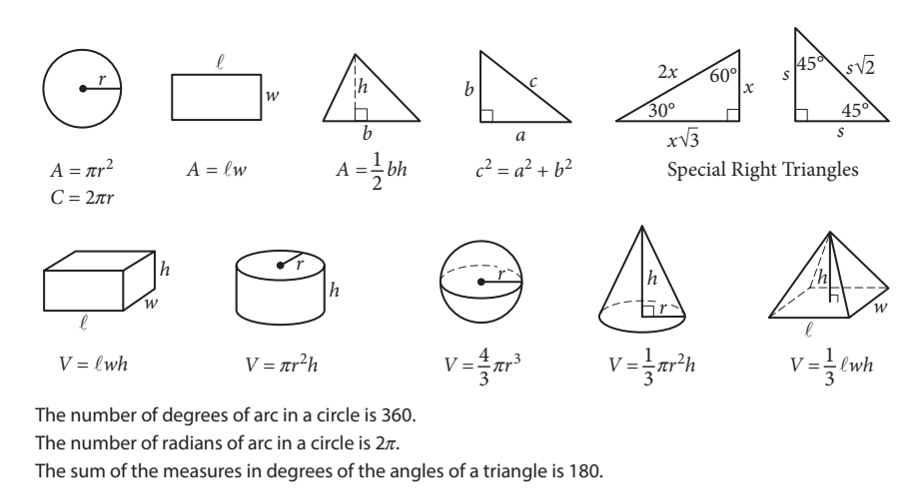
The SAT includes a reference sheet of useful formulas to help you answer questions on the exam. However, there are additional formulas that should also be known by student seeking the highest possible scores.

What's Included Already?

Below are the formulas that are included on the SAT exam. You should be familiar with which formulas are displayed here so that you know you can reference them when needed, but of course these formulas do not need to be memorized.

Below I will present additional formulas that are important to know.

Distance between two coordinate points

Given two points, $(x_1,y_1)$ and $(x_2,y_2)$ in the coordinate plane, the distance $d$ between the two points is given by

$$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

Note

Since the expressions in each set of parentheses are squared, the order in which you put in the points does not matter, as long as you keep $x$s with $x$s and $y$s with $y$s. All of the following are valid and equivalent formulas that will provide the same results.

$$\begin{array}{c}d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}\\ d=\sqrt{(x_2-x_1{)}^2+(y_1-y_2{)}^2}\\ d=\sqrt{(x_1-x_2{)}^2+(y_2-y_1{)}^2}\\ d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}\end{array}$$

Distance with Desmos

You can also compute the distance between two points by using the distance function. For example, to find the distance between the points $(1,2)$ and $(3,4)$, type into Desmos distance((1,2),(3,4)).

Slope between two coordinate points

Given two points, $(x_1,y_1)$ and $(x_2,y_2)$ in the coordinate plane, the slope $m$ of the line connecting the two points is given as follows.

$$m=\frac{y_2-y_1}{x_2-x_1}$$

Note

Since one can freely multiply both the numerator and denominator of any fraction by $-1$ without changing the value of the fraction, the positions of $x_1$ and $x_2$ along with $y_1$ and $y_2$ can be simultaneously swapped without changing the value that you end up computing. Both of the following are valid and equivalent formulas that will provide the same results.

$$\begin{array}{c}m=\frac{y_2-y_1}{x_2-x_1}\\ m=\frac{y_1-y_2}{x_1-x_2}\end{array}$$

Caution

Students often accidentally write $-$ in this formula as $+$. Remembering that slope derives from the notion of $\frac{\text{rise}}{\text{run}}$ and that the notions of $\text{rise}$ and $\text{run}$ are about changes or differences in $y$ and $x$ coordinates relative to one another can be helpful towards not making this mistake.

Midpoint of two coordinate points

Given two points, $(x_1,y_1)$ and $(x_2,y_2)$ in the coordinate plane, the midpoint of the two points (i.e. - the point halfway between these two points) has coordinates $(x_{\text{m}},y_{\text{m}})$ given by the following formula.

$$(x_{\text{m}},y_{\text{m}})=\left(\begin{array}{c}\text{average of}\\ \text{x coordinates}\end{array},\begin{array}{c}\text{average of}\\ \text{y coordinates}\end{array}\right)=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$$

Caution

Students often accidentally write $+$ in these formulas as $-$. Remembering that we are dealing with average values when computing a midpoint can be helpful towards not making this mistake.

Midpoint with Desmos

You can also compute the distance between two points by using the midpoint function. For example, to find the distance between the points $(1,2)$ and $(3,4)$, type into Desmos distance((1,2),(3,4)).

Slopes of Perpendicular Lines

If two lines with slopes $m_1$ and $m_2$ are perpendicular, then the slopes are negative reciprocals of each other

$$m_1=-\frac{1}{m_2}$$

or, equivalently,

$$m_1{m}_2=-1.$$

Forms of Equations of Lines

More information: Equations of Lines

There are three main forms of equations of lines that are useful to be familiar with.

Form	Equation	Unique?
Slope-Intercept	$y=mx+b$	Yes
Point-Slope	$y=m(x-h)+k$	No
Standard	$Ax+By=C$	No
For forms whose “Unique?” column lists “No,” there are multiple different ways to write the equation of the same line.

How to Interpret Each Constant

• $m$ is the slope of the line and is the same for slope-intercept form and point-slope form
• $(0,b)$ is the $y$-intercept of the line
• The line passes through the point $(h,k)$, which may be located anywhere in the $x$-$y$ plane.

Conversion Shortcuts

• To determine the value of $b$ ($y$ intercept), plug in $x=0$ and determine the resulting value of $b$.
  • Hence, for point-slope form, this would be $b=-mh+k$ and, for standard form, this would be $b=\frac{C}{B}.$
• To determine the slope $m$ from standard form, solve for $y$ and simplify into slope-intercept form.
  • The general result is $m=-\frac{A}{B}.$
• To convert into point-slope form, identify the slope $m$ and pick any point $(h,k)$ on your line.
• To convert into standard form, take an equation of your line and put all $x$ and $y$ terms on the same side of the equation. Put all non-$x$ and non-$y$ terms on the other side of the equation. Then, simplify completely.

Additional Note

• To determine the $x$ intercept, plug in $y=0$ and determine the resulting value of $x$.
  • Hence, for slope-intercept form, this would be $x=-\frac{b}{m},$ for point-slope form, this would be $x=-\frac{k}{m}+h,$ and for standard form, this would be $x=\frac{C}{A}.$

Equation of a Circle

More information: Circles

The equation of a circle of radius $r$ in the $x$-$y$ plane centered at the point $(h,k)$ is as follows.

$$(x-h{)}^2+(y-k{)}^2=r^2$$

Caution

Students often accidentally write $r$ instead of $r^2$ or accidentally write $-$ as $+$ in this formula. Noting that this equation is equivalent to the distance formula applied to the situation “the distance between the point $(x,y)$ and $(h,k)$ is $r$” can be helpful towards not making these mistakes.

Quadratic Formula

More information: Quadratic Formula

The solution to a general standard form quadratic equation $a{x}^2+bx+c=0$ is given by

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$$

This formula represents two solutions (one of the solutions takes $\pm$ as $+$ and the other takes $\pm$ as $-$).

The Discriminant

More information: The Quadratic Discriminant

The quantity $b^2-4ac$ found in the quadratic formula is called the discriminant of a quadratic equation. When $a$, $b$, and $c$ are real numbers, nowledge of this value being positive, negative, or zero can help inform us of the nature of the solutions to the corresponding quadratic equation $a{x}^2+bx+c=0$.

Discriminant	Nature of Solutions
$b^2-4ac>0$	Two distinct real solutions exist.
$b^2-4ac=0$	Only one real solution exists (a “double root”).
$b^2-4ac<0$	Solutions are complex and a conjugate pair. No real solutions exist.

Axis of Symmetry

The quantity $-\frac{b}{2a}$ found in the quadratic formula is the location of the axis of symmetry of a parabolic function. This is described in the section below as the quantity $h$.

Forms of Equations of Parabolas (Quadratic Functions)

More information: Quadratic Functions (Parabolas)

There are three main forms of equations of parabolas that are useful to be familiar with.

Form	Equation	Possible to write?*
Standard Form	$y=a{x}^2+bx+c$	Always possible
Vertex Form	$y=a(x-h{)}^2+c$	Always possible
Factored Form	$y=a(x-x_1)(x-x_2)$	Not always possible**

*This column describes whether or not the corresponding form of real-valued parabola equation is possible to write using only real numbers.

** Factored form is only possible to write if at least one $x$ intercept exists for the parabola.

How to Interpret Each Constant

• $a>0$ means the parabola is concave up and features a minimum; $a<0$ means the parabola is concave down and features a maximum
• $(0,c)$ is the $y$-intercept of the parabola
• $x=h$ is the equation of the axis of symmetry of the parabola
• $(h,k)$ are the coordinates of the vertex of the parabola (max/min point)
• $(x_1,0)$ and $(x_2,0)$ are the $x$ intercepts of the parabola, if they exist. In the case that the parabola only has one $x$ intercept at either its maximum or minimum point, $x_1$ and $x_2$ both hold the same value.

Conversion Shortcuts

• The value of $a$ is the same in all three forms.
• The value of $c$ ($y$ intercept) can be found from any form by plugging in $x=0$ and determining the value of $y$.
  • Hence, for vertex form, this would look like $c=a{h}^2+k$ and for factored form this would look like $c=a{x}_1{x}_2.$
• The values of $x_1$ and $x_2$ can be determined from standard form by means of the Quadratic Formula. These values can also be determined by identifying the $x$ intercepts of the graph when the function is graphable. Often, though, factored form can be obtained more quickly and reliably by factoring.
• The value of $h$ can be determined from standard form via $h=-\frac{b}{2a}.$
• The value of $h$ can be determined from factored form via computing the average of the $x$ intercepts: $h=\frac{x_1+x_2}{2}.$
• The value of $k$ can be determined from the value of $h$ by determining the $y$ value that results from plugging in $x=h$.
  • Hence, for standard form, this would look like $k=a{h}^2+bh+c$ and for factored form this would look like $k=a(h-x_1)(h-x_2).$
• The values of $h$ and $k$ can also be determined by identifying the vertex (max/min point) of the graph when the function is graphable. The coordinates of the vertex point are $(h,k)$.
• Standard form can easily be determined from vertex form and factored form by carrying out distribution and simplification.

Simple Exponential Growth/Decay & Compound Interest

Exponential functions take the form

$$y=a\cdot b^x$$

for positive values of $b$ only. The constants $a$ and $b$ have important interpretations.

• If $a>0$ then the values of $y$ will always be positive (the graph of this function will be above the $x$ axis).
• If $a<0$ then the values of $y$ will always be negative (the graph of this function will be below the $x$ axis).
• The $y$-intercept of the function is located at $(0,a)$.
• If $0<b<1$, then this function will describe exponential decay.
• If $b>1$, then this function will describe exponential growth.

Percentage Increase & Decrease

More information: Percentage Increase & Decrease

Use ratios of values to determine what percentage larger or smaller one value is compared to another. This is best seen through examples.

Example 1

Question: What percentage larger is $15$ than $12$?

Solution: $\frac{15}{12}=1.25=125\%=100\%+25\%$, so $15$ is $\boxed{25\%}$ larger than $12$.

Example 2

Question: What percentage smaller is $12$ than $15$?

Solution: $\frac{12}{15}=0.8=80\%=100\%-20\%$, so $12$ is $\boxed{20\%}$ smaller than $15.$

This is explained in much further detail on my page Percentage Increase & Decrease. These sorts of comparisons are very common on the SAT and also are unfortunately much trickier than they sem at first glance.

Geometric Definitions of Sine, Cosine, and Tangent (SOH CAH TOA)

For any right triangle, the longest side of the triangle is always called the hypotenuse. We often refer to the two remaining sides of the triangle relative to a chosen acute angle $\theta$ within the triangle. The side adjacent to the angle $\theta$ is often called the adjacent leg and the side that is neither the hypotenuse nor the adjacent leg is called the opposite leg. This is illustrated in the diagram below.

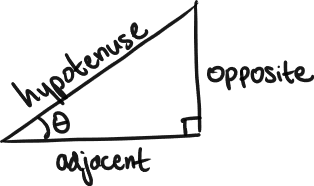
In mathematics, three important trigonometric functions, sine ($\sin$), cosine ($\cos$), and tangent ($\tan$) which use the angle $\theta$ as a variable describe ratios of side lengths of right triangles. The ratios that they describe are as follows.

$$\begin{array}{c}\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}\\ \cos \theta =\frac{\text{adjacent}}{\text{hypotenuse}}\\ \tan \theta =\frac{\text{opposite}}{\text{adjacent}}\end{array}$$

Often, the memory aid SOH CAH TOA is used to remember the sequences sine-opposite-hypotenuse, cosine-adjacent-hypotenuse, and tangent-opposite-adjacent in the formulas above.