Circles

A circle is a set of points in a plane that are at a fixed distance away from a chosen point, called the center of the circle. The fixed distance between the points of the circle and the center of the circle is called the radius $r$. The diameter $d$ is twice the magnitude of the radius $d=2r$ and represents the distance between opposing sides of the circle.

A pie-shaped portion of circle is called a sector.

$\pi$ (pi)

The number $3.14159265358979323846364\dots$ is a very important irrational number in mathematics that appears in formulas for the circumference and area of a circle. Like all irrational numbers, we cannot express this number in a compact decimal or fractional form. So, typically the Greek letter $\pi$ (pi) is used for simplicity in formulas.

$\pi$ is a built-in number available in all scientific and graphing calculators. For most general purposes, the approximation $\pi \approx 3.14$ suffices.

The irrational number $\pi$ (pi)

$\pi =3.14159265358979323846264\dots \approx 3.14$

$\pi$ also appears frequently when using radians to measure angles and in calculus courses.

Circumference (Perimeter) and Area

The perimeter of a circle is referred to as its circumference. The circumference $C$ of a circle with radius $r$ is given by the following formula.

Formula for the circumference of a circle

$$C=2\pi r$$

In terms of the diameter $d$, one can also write $C=\pi d$.

The area of a circle with radius $r$ is given by the following formula.

Formula for the area of a circle

$$A=\pi r^2$$

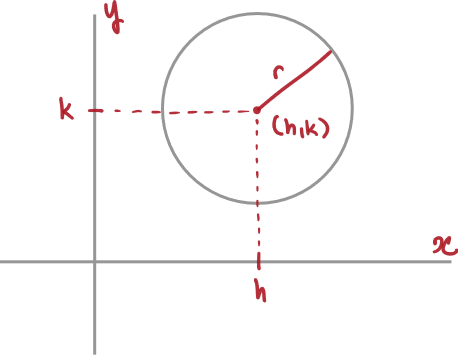
Equation in the $xy$-plane

The equation of a circle of radius $r$ and center $(h,k)$ in the $xy$-plane is given as follows.

Equation of a circle

$$(x-h{)}^2+(y-k{)}^2=r^2$$

Try graphing this yourself on Desmos, creating sliders for the variables $h$, $k$, and $r$ and play around by adjusting the values of the variables.

A sketch of the resulting circular graph is provided below.

Problems

Problem 1

Write the equation of the circle which has a diameter with endpoints at $(1,2)$ and $(-2,8)$.

Solution 1

The diameter $d$ of the circle is given by the distance between the two given points.

$$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}=\sqrt{(1-(-2){)}^2+(2-8{)}^2}=\sqrt{45}$$

The radius is half the length of the diameter.

$$r=\frac{d}{2}=\frac{\sqrt{45}}{2}$$

The center $(h,k)$ of the circle is located at the midpoint of the two given points.

$$(h,k)=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)=\left(\frac{1+(-2)}{2},\frac{2+8}{2}\right)=\left(-\frac{1}{2},5\right)$$

Plug this information into the general equation of the circle.

$$\begin{array}{c}(x-h{)}^2+(y-k{)}^2=r^2\\ {\left(x-\left(-\frac{1}{2}\right)\right)}^2+(y-5{)}^2={\left(\frac{\sqrt{45}}{2}\right)}^2\\ \boxed{{\left(x+\frac{1}{2}\right)}^2+(y-5{)}^2=\frac{45}{4}}\end{array}$$

Problem 2

Determine the radius and center of the circle given by $x^2-2x+y^2+4y=0.$

Solution 2

Adding $5$ to both sides allow us to factor into standard circle equation form.

$$\begin{array}{c}{x}^2-2x+1+y^2+4y+4=5\\ (x-1{)}^2+(y+2{)}^2=5\end{array}$$

Hence, the center of the circle is located at $\boxed{(1,-2)}$ and the radius is $\boxed{\sqrt{5}}$.

Problem 3

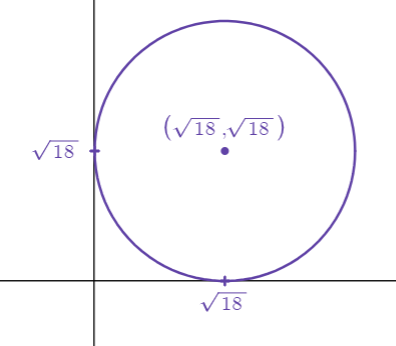
Write down the equation of the circle with area $18\pi$ and that lies tangent to the positive $x$ and $y$ axes (in other words, the circle overlaps the positive $x$ and $y$ axes each at only one point).

Solution 3

According to the area formula for a circle $A=\pi r^2,$ we have that $r^2=18,$ and so $r=\sqrt{18}.$ The $x$ and $y$ coordinates of the circle must also be $\sqrt{18}$ in order for the circle to lie tangent to the positive $x$ and $y$ axes.

$$\boxed{(x-\sqrt{18}{)}^2+(y-\sqrt{18}{)}^2=18}$$