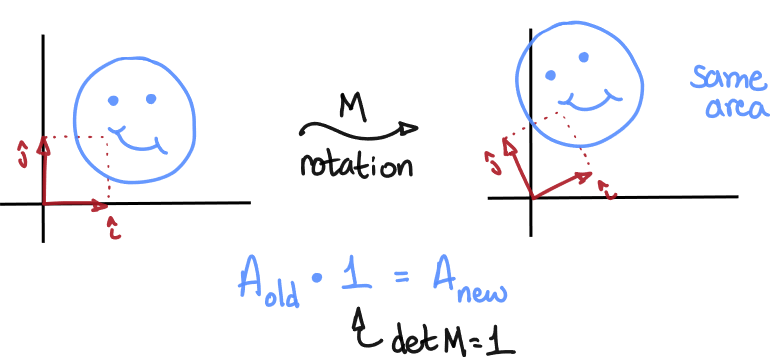Determinants

This topic is sometimes not covered in precalculus classes. It is more often included as a part of a linear algebra class covered in college. That being said, determinants of $2\times 2$ matrices does frequently appear as an ACT topic.

Conceptual Definition

Conceptual Definition of a Determinant

The determinant of a square matrix is a measure of the factor by which area (for $2\times 2$ matrices), volume (for $3\times 3$ matrices), etc. change under the matrix’s associated linear transformation. If the image of the transformation is mirrored, then the determinant is defined to be negative. If the original square matrix is $M$, then the determinant of that matrix is denoted by $\det M$.

Example 1 - determinant of a rotation matrix

If $M$ is a matrix whose corresponding linear transformation is a rotation, then $\boxed{\det M=1}$, since rotations preserve area and do not cause mirroring.

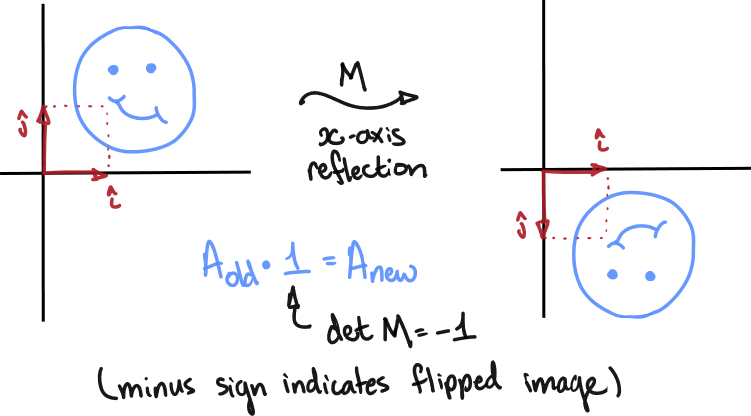
Example 2 - a negative determinant

If $M$ is a matrix whose corresponding linear transformation is a reflection across the $x$-axis, then $\boxed{\det M=-1}$, since reflections preserve area but do cause mirroring.

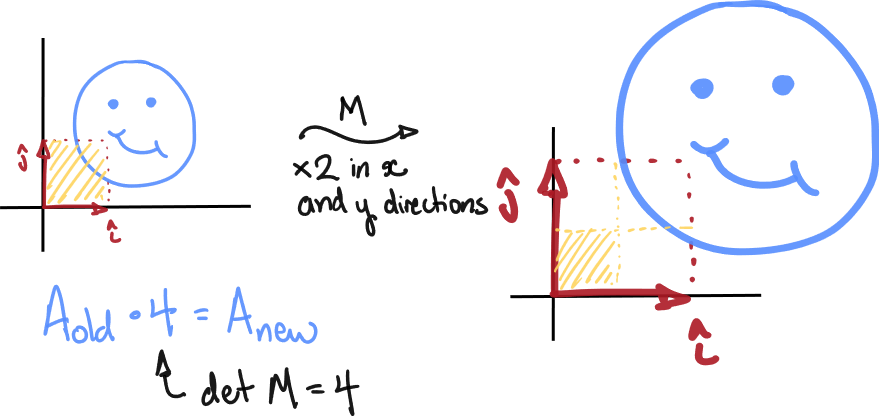
Example 3

If $M$ is a $2\times 2$ matrix whose corresponding linear transformation causes scaling along the $x$ and $y$ directions by a factor of $2$, then $\boxed{\det M=4}$, since areas are increased by a factor of $4$ but the transformation does not cause mirroring.

Example 4

If $M$ is a $3\times 3$ matrix whose corresponding linear transformation causes scaling along the $x,$ $y,$ and $z$ directions by a factor of $2$, then $\boxed{\det M=8}$, since volumes are increased by a factor of $8$ but the transformation does not cause mirroring.

Computational Definition

$2\times 2$ matrices

Below, I am providing a formula that can be used to compute the determinant of any $2\times 2$ matrix.

Computational Definition of the Determinant of a $2\times 2$ Matrix

The determinant of a $2\times 2$ is given as follows.

$$\det \left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=ad-bc$$

This formula is simple enough and useful enough to be worth memorizing.

Let’s try using this formula to compute the determinants of the matrix described in some of the conceptual examples.

Example 1 (revisited)

Consider the matrix

$$M=\left[\begin{array}{cc}\cos 20^{\circ }& \sin 20^{\circ }\\ -\sin 20^{\circ }& \cos 20^{\circ }\end{array}\right],$$

whose corresponding 2D transformation is a counterclockwise rotation by $20^{\circ }.$ The determinant of this matrix can then be computed as follows.

$$\det M={\cos }^{2}20^{\circ }-(-{\sin }^{2}20^{\circ })={\cos }^{2}20^{\circ }+{\sin }^{2}20^{\circ }\Rightarrow \boxed{\det M=1}$$

Example 2 (revsited)

Consider the matrix

$$M=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right],$$

whose corresponding 2D transformation is a reflection across the $x$ axis. The determinant of this matrix can then be computed as follows.

$$\det M=1\cdot (-1)-0\cdot 0\Rightarrow \boxed{\det M=-1}$$

These results are consistent with what we saw in the conceptual definition section.

$3\times 3$ matrices

Content coming soon

Larger matrices

Content coming soon