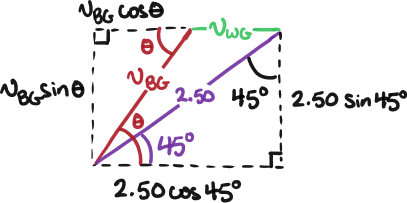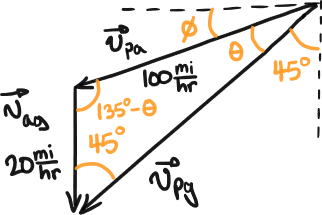Vectors

Problems titled “Giancoli” are sourced from Physics: Principles with Applications by Giancoli. A problem titled “Giancoli 3-P9,” for example, refers to problem 9 from chapter 3 (P refers to problem, Q refers to question).

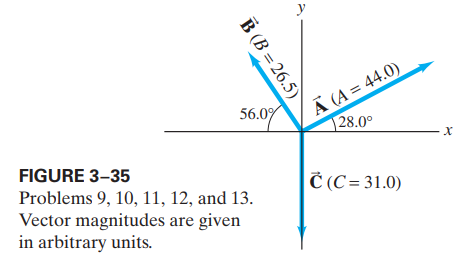
Giancoli 3-P9

Three vectors are shown in Fig. 3–35. Their magnitudes are given in arbitrary units. Determine the sum of the three vectors. Give the resultant in terms of (a) components (b) magnitude and angle with the $+x$ axis.

Solution to 3-P9

The components of the vectors are as follows.

$$\begin{array}{rl}& \\ \vec{\mathbf{A}}& =⟨44.0\cos 28.0^{\circ },44.0\sin 28^{\circ }⟩=⟨38.84969409\dots ,20.65674876\dots ⟩\\ \vec{\mathbf{B}}& =⟨-26.5\cos 56.0^{\circ },26.5\sin 56.0^{\circ }⟩=⟨-14.81861194\dots ,21.96949567\dots ⟩\\ \vec{\mathbf{C}}& =⟨0,-31.0⟩\end{array}$$

The sum found the vectors can be found by adding the components.

$$\vec{\mathbf{A}}+\vec{\mathbf{B}}+\vec{\mathbf{C}}=⟨A_x+B_x+C_x,A_y+B_y+C_y⟩$$ $$=⟨24.03108215\dots ,11.62624444\dots ⟩\approx \boxed{⟨24.0,11.6⟩\text{(a)}}$$

This vector lies in quadrant I. The magnitude and angle $\theta$ of the resultant vector can then be found using the Pythagorean theorem and tangent function, respectively.

$$|\vec{\mathbf{A}}+\vec{\mathbf{B}}+\vec{\mathbf{C}}|=\sqrt{24.03108215{\dots }^2+11.62624444{\dots }^2}=26.69573878\dots \approx \boxed{26.7\text{(b)}}$$ $$\tan \theta =\frac{y\text{-component}}{x\text{-component}}$$ $$\theta =\arctan \left(\frac{11.62624444\dots }{24.03108215\dots }\right)=\boxed{25.8^{\circ }\text{(b)}}$$

Giancoli 3-P16

You are given a vector in the $xy$ plane that has a magnitude of $90.0$ units and a $y$ component of $-65.0$ units. (a) What are the two possibilities for its $x$ component? (b) Assuming the $x$ component is known to be positive, specify the vector which, if you add it to the original one, would give a resultant vector that is $80.0$ units long and points entirely in the $-x$ direction.

Solution to 3-P16

Let’s call this vector $\vec{\mathbf{v}}=⟨v_x,v_y⟩$. We are told that $|\vec{\mathbf{v}}|=v=90.0$ and $v_y=-65.0$. The fact that $v_y<0$ restricts $\vec{\mathbf{v}}$ to only $\text{QIII}$ and $\text{QIV}.$ From this, we can compute one possible value for $\theta$, where $\theta$ is the angle between $\vec{\mathbf{v}}$ and the $+x$-axis, by taking advantage of the $\arcsin$ function.

$$v_y=v\sin \theta$$ $$\sin \theta =\frac{v_y}{v}$$ $$\theta =\arcsin \left(\frac{v_y}{v}\right)=\arcsin \left(\frac{-65.0}{90.0}\right)=-46.23825731{\dots }^{\circ }$$

This is a $\text{QIV}$ angle. The corresponding $\text{QIII}$ angle will have the same reference angle and can be found by computing

$$-180^{\circ }-(-46.23825731{\dots }^{\circ })=-133.7617427{\dots }^{\circ }$$

(Creating a sketch of the two possible angles may be helpful here.) Hence

$$\theta =\{-133.7617427{\dots }^{\circ },-46.23825731{\dots }^{\circ }\}.$$

From this, $v_x$ can be found.

$$\begin{array}{rl}{v}_x& =v\cos \theta =90.0\cos (-133.7617427{\dots }^{\circ })=-62.24949799\dots \text{ units}\\ v_x& =v\cos \theta =90.0\cos (-46.23825731{\dots }^{\circ })=62.24949799\dots \text{ units}\end{array}$$

Hence, $v_x=\boxed{\pm 62.2\text{ units (a)}}.$

For part (b), we are told to choose $\vec{\mathbf{v}}=⟨62.24949799\dots ,-65.0⟩$. We need a new vector $\vec{\mathbf{w}}$ such that the sum $\vec{\mathbf{s}}=\vec{\mathbf{v}}+\vec{\mathbf{w}}$ satisfies $\vec{\mathbf{s}}=⟨-80.0,0⟩$. The vector $\vec{\mathbf{w}}$ is then able to be found via subtraction.

$$\vec{\mathbf{w}}=\vec{\mathbf{s}}-\vec{\mathbf{v}}=⟨-80.0,0⟩-⟨62.24949799\dots ,-65.0⟩\approx \boxed{⟨-142.2,65.0⟩\text{(b)}}$$

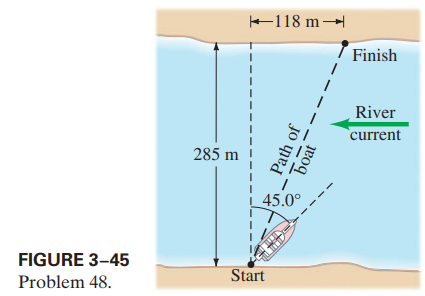
Giancoli 3-P48

A boat, whose speed in still water is $2.50\text{m/s}$, must cross a $285\text{m}$-wide river and arrive at a point $118\text{m}$ upstream from where it starts (Fig. 3–45). To do so, the pilot must head the boat at a $45.0^{\circ }$ upstream angle. What is the speed of the river’s current?

Hint for 3-P48

For this problem, let the velocity of the water relative to the ground be ${\vec{\mathbf{v}}}_{\text{wg}},$ the velocity of the boat relative to the water be ${\vec{\mathbf{v}}}_{\text{bw}},$ and the velocity of the boat relative to the ground be ${\vec{\mathbf{v}}}_{\text{bg}}.$ The relationship between these three vectors is

$${\vec{\mathbf{v}}}_{\text{bw}}+{\vec{\mathbf{v}}}_{\text{wg}}={\vec{\mathbf{v}}}_{\text{bg}}.$$

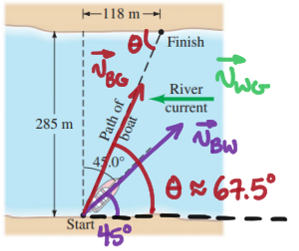
Solution to 3-P48

Let’s begin by labeling the velocity vectors identified in the hint. In the paragraph below the image I will describe how I computed the value of $\theta$.

Note that the vector ${\vec{\mathbf{v}}}_{\text{bg}}$ points directly from the start point to the finish point. The angle $\theta$ between this vector is computable by identifying its opposite and adjacent sides in the right triangle formed by the dotted lines and using the $\arctan$ function.

$$\theta =\arctan \left(\frac{285\text{m}}{118\text{m}}\right)=67.50872885{\dots }^{\circ }$$

Let’s summarize the information that we have available now. Unknown magnitudes are indicated with "$??$".

• ${\vec{\mathbf{v}}}_{\text{bw}}=2.50,\text{ at }45^{\circ }$
• ${\vec{\mathbf{v}}}_{\text{wg}}=??,\text{ at }180^{\circ }$
• ${\vec{\mathbf{v}}}_{\text{bg}}=??,\text{ at }67.50872885{\dots }^{\circ }$

Here’s a sketch of these three vectors with a shared origin.

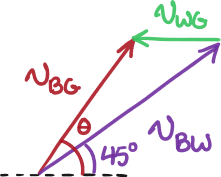
Next, let’s arrange them into a tip-to-tail diagram in accordance with the relationship ${\vec{\mathbf{v}}}_{\text{bw}}+{\vec{\mathbf{v}}}_{\text{wg}}={\vec{\mathbf{v}}}_{\text{bg}}.$

Finally, let’s break down the diagonal vectors (${\vec{\mathbf{v}}}_{\text{bw}}$ and ${\vec{\mathbf{v}}}_{\text{bg}}$) into components and also get rid of the vector arrows for simplicity. I also went ahead and labeled the components themselves in terms of the hypotenuses of their respective right triangles by using the $\sin$ and $\cos$ functions.

Remember, $\theta$ is already known (see above), so there are only two unknowns: $v_{\text{bg}}$ and $v_{\text{wg}}$. The question asks us to find $v_{\text{wg}}$. So, we will use the diagram to write a system of two equations and eliminate $v_{\text{bg}}$ in order to solve for $v_{wg}$.

Using the most recent diagram, we can equate the vertical sides and horizontal sides of the big rectangle in order to get our two equations.

$$\{\begin{array}{ll}{v}_{\text{bg}}\sin \theta =2.50\sin 45^{\circ }& \text{vertical}\\ v_{\text{bg}}\cos \theta +v_{\text{wg}}=2.50\cos 45^{\circ }& \text{horizontal}\end{array}$$

Let’s solve for $v_{\text{bg}}$ via the vertical equation.

$$v_{\text{bg}}=\frac{2.50\sin 45^{\circ }}{\sin \theta }=\frac{2.50\sin 45^{\circ }}{\sin (67.50872885{\dots }^{\circ })}=1.913296447\dots$$

Now, substitute this into the horizontal equation and solve for $v_{\text{wg}}$.

$$\begin{array}{rl}{v}_{\text{wg}}& =2.50\cos 45^{\circ }-v_{\text{bg}}\cos \theta \\ & =2.50\cos 45^{\circ }-(1.913296447\dots )\cos (67.50872885{\dots }^{\circ })\\ & =1.035849408\approx \boxed{1.03\frac{\text{m}}{\text{s}}}\end{array}$$

Giancoli 3-P52

Two vectors, ${\vec{V}}_1$ and ${\vec{V}}_2$, add to a resultant ${\vec{V}}_R={\vec{V}}_1+{\vec{V}}_2$. Describe ${\vec{V}}_1$ and ${\vec{V}}_2$ if (a) $V_R=V_1+V_2$, (b) $V_R^2=V_1^2+V_2^2$, (c) $V_1+V_2=V_1-V_2$.

Solution to 3-P52

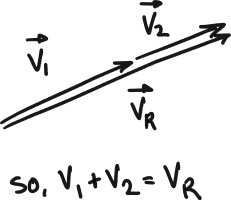
(a) ${\vec{V}}_1$ and ${\vec{V}}_2$ point in the same direction. This is easily seen through the tip-to-tail diagram below.

Note

This is the most extreme case of the triangle inequality. The triangle inequality in general guarantees that $V_R\le V_1+V_2$ regardless of the details of ${\vec{V}}_1$ and ${\vec{V}}_2$. The inequality sign turns into an inequality when the two vectors ${\vec{V}}_1$ and ${\vec{V}}_2$ point in the same direction.

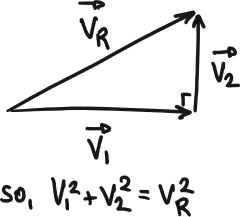
(b) ${\vec{V}}_1$ and ${\vec{V}}_2$ are perpendicular to each other. This guarantees that the Pythagorean theorem can be applied to the tip-to-tail diagram representing the sum ${\vec{V}}_R={\vec{V}}_1+{\vec{V}}_2,$ as shown in the diagram below.

(c) Subtracting $V_1$ from both sides of $V_1+V_2=V_1-V_2$ gives $V_2=-V_2$, which hence implies $V_2=0$. This therefore means that ${\vec{V}}_2$ must have zero length (the magnitude of ${\vec{V}}_2$ must be zero).

Problem

You are flying a plane and want to go from City A to City B. City A is located northeast of City B and are $200\text{mi}$ apart. Your plane has an engine that can provide thrust for a speed of $100\frac{\text{mi}}{\text{hr}}$. There is wind oriented south with a speed of $20\frac{\text{mi}}{\text{hr}}$.

(a) in which direction do you need to aim the plane?

(b) how long does it take you to get to city B?

Solution

In this relative velocity problem, the three objects of concern are the plane, the air, and the ground.

• In order to go from City A to City B, one needs to travel southwest since City A is northeast of city B. Since the cities are located on the ground, this indicates to us the direction of the velocity of the plane relative to the ground ${\vec{v}}_{pg}$ is southwest.
• We are told that the wind is travelling at $20\frac{\text{mi}}{\text{hr}}$ in the southern direction, which can be interpreted as the velocity of the air relative to the ground ${\vec{v}}_{ag}.$
• We are told that the engines of the plane can provide the plane with a speed of $100\frac{\text{mi}}{\text{hr}}$ relative to the air.

Let’s summarize the three velocities and the information we know about them. Some information is unknown, which is kept blank in the table.

Velocity of…	Symbol	Magnitude	Direction
plane rel. to ground	${\vec{v}}_{pg}$		southwest
air rel. to ground	${\vec{v}}_{ag}$	$20\frac{\text{mi}}{\text{hr}}$	south
plane rel. to air	${\vec{v}}_{pa}$	$100\frac{\text{mi}}{\text{hr}}$

These velocities will add as follows.

$${\vec{v}}_{pa}+{\vec{v}}_{ag}={\vec{v}}_{pg}$$

The information in the table can be arranged in a tip-to-tail vector addition diagram as shown below.

Use the law of sines to compute the angle $\theta$ and thus $\varphi$.

$$\begin{array}{c}\frac{100}{\sin 45^{\circ }}=\frac{20}{\sin \theta }\\ \theta =\arcsin \left(\frac{20\sin 45^{\circ }}{100}\right)=8.130102354{\dots }^{\circ }\\ \varphi =45^{\circ }-\theta \approx 37^{\circ }\end{array}$$

Hence, the direction of ${\vec{v}}_{pa}$ is approximately $\boxed{37^{\circ }\text{south of west (a),}}$ which is the direction that the plane needs to be aimed.

The magnitude of ${\vec{v}}_{pg}$ can then be found through the law of sines.

$$\begin{array}{c}\frac{|{\vec{v}}_{pg}|}{\sin (135^{\circ }-\theta )}=\frac{100}{\sin 45^{\circ }}\\ |{\vec{v}}_{pg}|=\frac{100\sin (135^{\circ }-\theta )}{\sin 45^{\circ }}=113.137085\frac{\text{mi}}{\text{hr}}\end{array}$$

Since the two cities are $200\text{mi}$ apart, the amount of time required is

$$\text{time}=\frac{200\text{mi}}{|{\vec{v}}_{pg}|}=1.767\dots \approx \boxed{1\text{hr}46\text{min (b)}.}$$