Factorials

Definition for Factorials of Natural Numbers

A factorial of some natural number $n$, written as $n!$ and read as ”$n$ factorial,” is the product of all natural numbers less than or equal to $n$.

Definition of Factorials of Natural Numbers

If $n$ is a natural number, then

$$n!=n\cdot (n-1)\cdots 4\cdot 3\cdot 2\cdot 1=\left(\begin{array}{c}\text{the product of all}\\ \text{natural numbers ≤n}\end{array}\right).$$

Below are the computations of the first few factorials.

$$\begin{array}{rl}5!& =5\cdot 4\cdot 3\cdot 2\cdot 1=120\\ 4!& =4\cdot 3\cdot 2\cdot 1=24\\ 3!& =3\cdot 2\cdot 1=6\\ 2!& =2\cdot 1=2\\ 1!& =1\end{array}$$

Permutations of a Set of Elements

One of the most fundamental motivations for defining the factorial $n!$ of a natural number $n$ is to represent the number of permutations (orderings) of $n$ objects in a sequence. For example, the five letters ABCDE can be arranged in $5!=120$ different orderings (ABCDE, EDACB, BADCE, etc).

Why?

In order to count the number of ways to order the five letters ABCDE, imagine beginning with five different empty slots that we are going to fill in with letters.

$$\underline{}\underline{}\underline{}\underline{}\underline{}$$

Let’s work left to right. There are five different letter options that we can put into the first slot (A, B, C, D, and E).

$$\underline{(5)}\underline{}\underline{}\underline{}\underline{}$$

Now that one letter has been used in the first slot, there remain only four possible letters that can go into the second slot. Similarly, only three letter options remain for the third slot and so on.

$$\underline{(5)}\underline{(4)}\underline{(3)}\underline{(2)}\underline{(1)}$$

Five choices followed by four choices followed by three choices followed by two choices followed by 1 choice makes for $5\cdot 4\cdot 3\cdot 2\cdot 1=120$ distinct overall choices, which is exactly what we have defined as $5!$.

We will return to this example of distinct permutations of the letters ABCDE in the next section.

Definition of $0!$

The above definition does not provide for a straightforward way to reason about the value of $0!$, though needing to compute this value is not uncommon, particularly when solving problems in probability, computing combinations and permutations, or constructing power series.

Definition of $0!$

$$0!=1$$

Why?

Based on the first few factorials listed above, we notice the following pattern.

$$\begin{array}{rl}4!& =5!÷5\\ 3!& =4!÷4\\ 2!& =3!÷3\\ 1!& =2!÷2\end{array}$$

Thus, the continuation of this pattern suggests that $0!=1!÷1=1$. This result works in expected ways among a variety of formulas in which the notion of a factorial is used, so we take $0!=1$ as the definition of $0!.$

Including this definition for $0!$ now provides us with an understanding of how to compute the factorial of any nonnegative integer.

Let’s return back now to the task of determining the number of ways to distinctly permute (order) the letters ABCDE. The number of ways to arrange the letters ABCDE can be thought of the number of ways to permute five elements out of a set of five, or in other words ${}_5{P}_5$. According to the formula for permutations, this is given as follows.

$${}_5{P}_5=\frac{5!}{(5-5)!}=\frac{5!}{0!}=\frac{5!}{1}=5!=120$$

This result is consistent with the results of the previous section, but raises two noteworthy points:

• In order to compute ${}_5{P}_5$ using the factorial-based formula, we needed to use the definition $0!=1$. This value indeed provides the expected results when working with the permutations formula above.
• Extending the result that we see here for $n=5$, we find that evidently, for any nonnegative integer, we get ${}_n{P}_n=n!$.

Definition for All Other Numbers

For calculus students who are familiar with improper integrals, the factorial can be extended to other numbers (including fractional numbers, irrational numbers, and complex numbers) via an integral.

Integral Definition of the Factorial of Any Value of $n$

$$n!={\int }_0^{\infty }{x}^n{e}^{-x}dx$$

Remark: Copy-paste the code \int_0^\infty x^n e^{-x} dx to compute values of this integral in Desmos. Don’t forget to add a slider for $n$.

(In textbooks, the Gamma function is often used instead of the above definition, but I’m omitting that explanation here because there is an annoying subtle difference between the Gamma function and the factorial that in my opinion has no practical value.)

I strongly recommend trying to verify the following facts that follow from this definition.

1. $0!=1$
2. For any $n\ge 0$, $(n+1)!=(n+1)\cdot n!$ (this requires integration by parts)

These two facts together are what ensure that the definition above agrees with the definition for factorials of nonnegative integers mentioned earlier in this article (why is this so?). Try verifying that the integral and factorial values agree with each other using a calculator of your choice and a value of $n$ of your choice.

Additionally, the integral definition shown in the box above provides the same values that calculators give for factorials of nonnegative integers (such as Desmos and TI calculators).

Miscellaneous remarks:

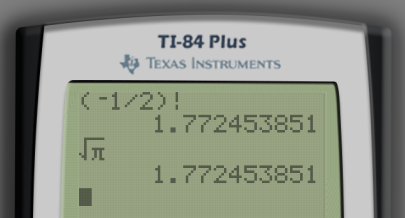
• This integral definition does yield some unexpected results, such as the famous factorial of $\frac{1}{2}$, which is related to $\pi$. Try verifying the result below with your calculator (use the integral definition as well as built-in factorial functionality as a sanity check). $$\left(\frac{1}{2}\right)!=\frac{\sqrt{\pi }}{2}=0.8862269255\dots$$ It is not easy to show that this result follows from the integral definition of the factorial but nonetheless the result is true.
• This integral does not converge for any negative integer $n$, which in general means that $n!$ is undefined for any negative integer $n$. When graphing $y=x!$, one can see vertical asymptotes at all of the negative integer values of $x$, which reflects this fact.

From the property $(n+1)!=(n+1)\cdot n!$ and the integral definition of the factorial given in the box above, the values of the factorial of any negative number can be extrapolated as illustrated in the example below.

Example

Given that $\left(\frac{1}{2}\right)!=\frac{\sqrt{\pi }}{2}$, show that $\left(-\frac{1}{2}\right)!=\sqrt{\pi }.$

Solution

$$\begin{array}{rlr}(n+1)!& =(n+1)\cdot n!& \text{established property}\\ \left(\frac{1}{2}\right)!& =\frac{1}{2}\cdot \left(-\frac{1}{2}\right)!& \text{set }n=\frac{1}{2}\\ \frac{\sqrt{\pi }}{2}& =\frac{1}{2}\cdot \left(-\frac{1}{2}\right)!& \text{substitute }\left(\frac{1}{2}\right)!=\frac{\sqrt{\pi }}{2}\\ \sqrt{\pi }& =\left(-\frac{1}{2}\right)!& \text{multiply both sides by }2\end{array}$$

The proof is now complete. A sanity check of this result can be provided with the help of a calculator.