Dot Products

Definition in Terms of Vector Magnitudes and Angles

The dot product $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}$ of two vectors $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ is defined in terms of the vector magnitudes $a$ and $b$ as well as the angle between the vectors $\theta$.

Definition of a Dot Product

$$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=ab\cos \theta$$

This definition holds for vectors in any number of dimensions. Since $a$ and $b$ are positive, the sign of $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}$ depends on the angle $\theta$ according to the following table.

Sign of $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}$	Angle between $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$
$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}>0$	acute ($0^{\circ }\le \theta <90^{\circ }$)
$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=0$	right ($\theta =90^{\circ }$)
$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}<0$	obtuse ($90^{\circ }<\theta \le 180^{\circ }$)

Practice Problems

Problem 1

Let $\vec{\mathbf{v}}$ and $\vec{\mathbf{w}}$ be vectors in the $xy$-plane with magnitudes and angles measured counterclockwise from the positive $x$-axis. The magnitude of $\vec{\mathbf{v}}$ is $6$, and its angle is $40^{\circ }$. The magnitude of $\vec{\mathbf{w}}$ is $3$, and its angle is $160^{\circ }$. Determine $\vec{\mathbf{v}}\cdot \vec{\mathbf{w}}$.

Solution 1

The angle between the two vectors is $\theta =160^{\circ }-40^{\circ }=120^{\circ }.$ Hence $\cos \theta =\cos 120^{\circ }=-\frac{1}{2}$ (precalc students are often expected to recall this value from memory but it can also be found with a calculator). So, the dot product is

$$\vec{\mathbf{v}}\cdot \vec{\mathbf{w}}=vw\cos 120^{\circ }=6\cdot 3\cdot \left(-\frac{1}{2}\right)=\boxed{-9}.$$

Problem 2

Fill in the multiplication table below for dot products between the 3D unit vectors $\hat{ı},$ $\hat{ȷ},$ and $\hat{k}.$

$$\begin{array}{cccc}\cdot & \hat{ı}& \hat{ȷ}& \hat{k}\\ \hat{ı}& & & \\ \hat{ȷ}& & & \\ \hat{k}& & & \end{array}$$

Solution 2

Recall that $|\hat{ı}|=|\hat{ȷ}|=|\hat{k}|=1$ and that $\hat{ı},$ $\hat{ȷ},$ and $\hat{k}$ are all mutually perpendicular (meaning that they each have an angle of $90^{\circ }$ with each other). We can compute each dot product in the following fashion.

• $\hat{ı}\cdot \hat{ı}=|\hat{ı}||\hat{ı}|\cos 0^{\circ }=1\cdot 1\cdot 1=1$
• $\hat{ı}\cdot \hat{ȷ}=|\hat{ı}||\hat{ȷ}|\cos 90^{\circ }=1\cdot 1\cdot 0=0$
• etc.

This results in the table of values shown below.

$$\begin{array}{cccc}\cdot & \hat{ı}& \hat{ȷ}& \hat{k}\\ \hat{ı}& 1& 0& 0\\ \hat{ȷ}& 0& 1& 0\\ \hat{k}& 0& 0& 1\end{array}$$

Computation in Terms of Components

The dot product can also be very conveniently computed in terms of the two-dimensional components of $\vec{\mathbf{a}}=⟨a_x,a_y⟩$ and $\vec{\mathbf{b}}=⟨b_x,b_y⟩$ according to the following theorem.

Theorem: Computing a Dot Product in Terms of Vector Components (2D)

$$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=a_x{b}_x+a_y{b}_y$$

Why?

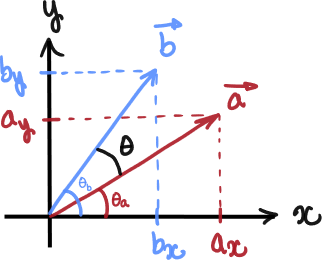
Let $\vec{\mathbf{a}}=⟨a_x,a_y⟩$ and $\vec{\mathbf{b}}=⟨b_x,b_y⟩$ be vectors with angles ${\theta }_a$ and ${\theta }_b$ defined with respect to the $+x$ axis in the conventional manner as shown in the diagram below.

Note that from this we have the traditional formulas for the components of $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}.$

$$\{\begin{array}{l}{a}_x=a\cos {\theta }_a\\ a_y=a\sin {\theta }_a\end{array}\text{and}\{\begin{array}{l}{b}_x=b\cos {\theta }_b\\ b_y=b\sin {\theta }_b\end{array}$$

Based on the picture, we can see that the angle between the vectors $\theta$ is related to ${\theta }_a$ and ${\theta }_b$ through $\theta ={\theta }_b-{\theta }_a.$ This allows us to rewrite $ab\cos \theta$ in terms of the components of $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ by means of the cosine of a difference formula (see step marked $\star$).

$$\begin{array}{rlr}\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}& =ab\cos \theta & \\ & =ab\cos ({\theta }_a-{\theta }_b)& \\ & =ab(\cos {\theta }_a\cos {\theta }_b+\sin {\theta }_a\sin {\theta }_b)& \star \\ & =\underset{a_x}{\underbrace{a\cos {\theta }_a}}\underset{b_x}{\underbrace{b\cos {\theta }_b}}+\underset{a_y}{\underbrace{a\sin {\theta }_a}}\underset{b_x}{\underbrace{b\sin {\theta }_b}}& \\ & =a_x{b}_x+a_y{b}_y✓& \end{array}$$

Practice Problems

Problem 1

Find the value of $\alpha$ for which $\vec{\mathbf{a}}=5\hat{ı}-2\alpha \hat{ȷ}+2\hat{k}$ is perpendicular to the vector $\vec{\mathbf{b}}=\hat{ı}-\hat{ȷ}$.

Solution 1

We know the dot product of perpendicular vectors vanishes. This can be used to set up an equation which can be solved for $\alpha .$

$$\begin{array}{c}\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=0\\ 5\cdot 1+(-2\alpha )\cdot (-1)+2\cdot 0=0\\ 5+2\alpha =0\\ \boxed{\alpha =-\frac{5}{2}}\end{array}$$

Problem 2

Find all the numbers $x$ for which $x\hat{ı}+3\hat{ȷ}+\hat{k}$ is perpendicular to the vector $x\hat{ı}-3x\hat{ȷ}+20\hat{k}$.

Solution 2

We know the dot product of perpendicular vectors vanishes. This can be used to set up an equation which can be solved for $x.$

$$\begin{array}{c}(x\hat{ı}+3\hat{ȷ}+\hat{k})\cdot (x\hat{ı}-3x\hat{ȷ}+20\hat{k})=0\\ x\cdot x+3\cdot (-3x)+1\cdot 20=0\\ x^2-9x+20=0\\ (x-4)(x-5)=0\\ \boxed{x=\{4,5\}}\end{array}$$

Problem 3

For $\vec{\mathbf{a}}=⟨2,-1,-2⟩$ and $\vec{\mathbf{b}}=⟨3,2,-1⟩$, calculate the cosine of the angle between the two vectors.

Solution 3

$$\begin{array}{c}\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=|\vec{\mathbf{a}}||\vec{\mathbf{b}}|\cos \theta \\ \cos \theta =\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{|\vec{\mathbf{a}}||\vec{\mathbf{b}}|}\\ \cos \theta =\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{\sqrt{a_x^2+a_y^2+a_z^2}\sqrt{b_x^2+b_y^2+b_z^2}}\\ \cos \theta =\frac{2\cdot 3+(-1)\cdot 2+(-2)\cdot (-1)}{\sqrt{2^2+1^2+2^2}\sqrt{3^2+2^2+1^2}}=\boxed{\frac{\sqrt{14}}{7}}=\boxed{0.534\dots }\end{array}$$

Problem 4

Find the 2D vectors of magnitude $3$ perpendicular to $⟨2,-5⟩$. (Don’t worry about rationalizing denominators.)

Solution 4

Since the dot products of perpendicular vectors vanish, we want to find a vector $⟨x,y⟩$ such that $⟨x,y⟩\cdot ⟨2,-5⟩=0$. This yields the following equation, which is the equation of a line in the $xy$ plane that passes through the origin.

$$2x-5y=0$$

We want $⟨x,y⟩$ to have magnitude $3$, or in other words $|⟨x,y⟩|=3,$ so

$$\begin{array}{c}\sqrt{x^2+y^2}=3,\\ x^2+y^2=9,\end{array}$$

which is the equation of the circle in the $xy$ plane centered at the origin with radius $3$. From the equation of the line, we get $y=\frac{2}{5}x$, which can be substituted into the equation of the circle in order to find $x$.

$$\begin{array}{c}{x}^2+{\left(\frac{2}{5}x\right)}^2=9\\ \frac{29}{25}{x}^2=9\\ x=\pm \frac{15}{\sqrt{29}}\end{array}$$

The corresponding $y$ components are given by $y=\frac{2}{5}x$.

$$y=\pm \frac{6}{\sqrt{29}}$$

The final result is thus as follows.

$$⟨x,y⟩=\boxed{⟨\pm \frac{15}{\sqrt{29}},\pm \frac{6}{\sqrt{29}}⟩}$$

Problem 5

Consider the vectors $\vec{\mathbf{v}}=⟨1,2,3⟩$ and $\vec{\mathbf{w}}=⟨-3,4,-1⟩.$

(a) Determine if the angle between these two vectors is acute, right, or obtuse.

(b) State a 3D vector that is perpendicular to both

Solution 5

(a) Since

$$\vec{\mathbf{v}}\cdot \vec{\mathbf{w}}=1\cdot (-3)+2\cdot 4+3\cdot (-1)=2,$$

which is a positive value, we must have that the angle between these two vectors is $\boxed{\text{acute}}.$

(b) We now seek a vector $⟨x,y,z⟩$ that is perpendicular to both $\vec{\mathbf{v}}$ and $\vec{\mathbf{w}}$. The dot product with both $\vec{\mathbf{v}}$ and $\vec{\mathbf{w}}$ hence must vanish.

$$\{\begin{array}{l}⟨x,y,z⟩\cdot \vec{\mathbf{v}}=0\\ ⟨x,y,z⟩\cdot \vec{\mathbf{w}}=0\end{array}$$ $$\{\begin{array}{l}x+2y+3z=0\\ -3x+4y+-z=0\end{array}$$

So, we need to state any vector $⟨x,y,z⟩$ that satisfies both of these equations. In order to do this, let’s eliminate one of the variables. For our purposes here, we will eliminate $x.$ From the first equation, we have $x=-2y-3z$ and substituting this into the second equation gives the following, which I simplified by solving for $z.$

$$\begin{array}{c}-3(-2y-3z)+4y-z=0\\ 6y+9z+4y-z=0\\ 10y+8z=0\\ z=-\frac{5}{4}y\end{array}$$

Hence, $x=-2y-3(-\frac{5}{4}y)=\frac{7}{4}y$ and so any vector of the form

$$⟨\frac{7}{4}y,y,-\frac{5}{4}y⟩$$

will work (you can pick any nonzero value of $y$ that you’d like and if you plug it into the above it will be perpendicular to both $\vec{\mathbf{v}}$ and $\vec{\mathbf{w}}$). As an example, pick $y=1$, we get $\boxed{⟨\frac{7}{4},1,-\frac{5}{4}⟩}$, but of course there are an infinite number of solutions, so yours may not match.

How can I check if my answer is correct? Does your $⟨x,y,z⟩$ answer satisfy $x=\frac{7}{4}y$ and $z=-\frac{5}{4}y$? If so, then your example works!

Formula in three dimensions

The dot product can be computed in terms of the three-dimensional components of $\vec{\mathbf{a}}=⟨a_x,a_y,a_z⟩$ and $\vec{\mathbf{b}}=⟨b_x,b_y,b_z⟩.$

Theorem: Computing a Dot Product in Terms of Vector Components (3D)

$$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=a_x{b}_x+a_y{b}_y+a_z{b}_z$$

Notice how elegantly this extends the two-dimensional formula into three dimensions. One of the big reasons why dot products have been established as their own object is due to the simplicity that is associated with their computation despite having nontrivial tie to the original vectors still given by $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=ab\cos \theta .$

Practice Problem

Problem

Show that if $\vec{\mathbf{a}}=⟨a_x,a_y,a_z⟩$, then $\vec{\mathbf{a}}\cdot \hat{ı}=a_x$.

Solution

Recalling that $\hat{ı}$ denotes the unit vector pointing in the $+x$ direction, we know that $\hat{ı}=⟨1,0,0⟩.$ According to the theorem,

$$\vec{\mathbf{a}}\cdot \hat{ı}=a_x\cdot 1+a_y\cdot 0+a_z\cdot 0=a_x.✓$$

Properties of Dot Products

Properties of Dot Products

Let $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ be arbitrary vectors and $k$ be any constant. Then, the commutative, distributive, and assosciative properties of dot products hold as described in the table below.

Property	Details
Commutative Property	$\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=\vec{\mathbf{b}}\cdot \vec{\mathbf{a}}$
Distributive Property	$\vec{\mathbf{a}}\cdot (\vec{\mathbf{b}}+\vec{\mathbf{c}})=\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}+\vec{\mathbf{a}}\cdot \vec{\mathbf{c}}$
Assosciative Property	$(k\vec{\mathbf{a}})\cdot \vec{\mathbf{b}}=k(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})$

Computing Projections with Dot Products

The projection of $\vec{\mathbf{a}}$ on $\vec{\mathbf{b}}$, denoted ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$ is the component of $\vec{\mathbf{a}}$ in the direction of $\vec{\mathbf{b}}$.

The projection of a vector $\vec{\mathbf{a}}$ on a second vector $\vec{\mathbf{b}}$, denoted as ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$, can be found through a dot product by means of the following formula.

Projection of Vector $\vec{\mathbf{a}}$ on Vector $\vec{\mathbf{b}}$.

$${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}=\frac{(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})\vec{\mathbf{b}}}{b^2}$$

Why?

If $\theta$ is the angle between $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ then $|{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}|=a\cos \theta =\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{b}$. The direction of ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$ is the same as $\vec{\mathbf{b}}$. The unit vector that points in the direction of $\vec{\mathbf{b}}$ is $\hat{b}=\frac{\vec{\mathbf{b}}}{b}.$ From this, we can construct the formula for ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$.

$${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}=|{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}|\hat{b}=\left(\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{b}\right)\left(\frac{\vec{\mathbf{b}}}{b}\right)=\frac{(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})\vec{\mathbf{b}}}{b^2}✓$$

Practice Problems

Problem 1

Compute ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$ if $\vec{\mathbf{a}}=⟨2,3,-1⟩$ and $\vec{\mathbf{b}}=⟨4,-3,1⟩.$

Solution 1

First, compute $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}$ and $b^2$.

$$\begin{array}{c}\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=a_x{b}_x+a_y{b}_y+a_z{b}_z=2\cdot 4+3\cdot (-3)+(-1)\cdot 1=-2\\ b^2=b_x^2+b_y^2+b_z^2=4^2+3^2+1^2=26\end{array}$$

Use these results to compute the projection vector.

$$\begin{array}{c}{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}=\frac{(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})\vec{\mathbf{b}}}{b^2}\\ {\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}=\frac{-2⟨4,-3,1⟩}{26}=\boxed{⟨\frac{4}{13},-\frac{3}{13},\frac{1}{13}⟩}\end{array}$$

Problem 2

Show that if $\vec{\mathbf{u}}=\vec{\mathbf{a}}-{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$, and neither $\vec{\mathbf{u}}$ or $\vec{\mathbf{b}}$ are the zero vector, then $\vec{\mathbf{u}}$ is perpendicular to $\vec{\mathbf{b}}$.

Solution 2 Method 1

Based on the definition of $\vec{\mathbf{u}}$, we have that $\vec{\mathbf{a}}=\vec{\mathbf{u}}+{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}.$ This means that $\vec{\mathbf{u}}$ can be included in a vector diagram with $\vec{\mathbf{a}},$ $\vec{\mathbf{b}},$ and ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}$ as follows.

From this diagram, it is clear that $\vec{\mathbf{u}}\perp \vec{\mathbf{b}}.$

Solution 2 Method 2

Let’s compute $\vec{\mathbf{u}}\cdot \vec{\mathbf{b}}$ and expand using the formula for ${\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}}.$

$$\begin{array}{rl}\vec{\mathbf{u}}\cdot \vec{\mathbf{b}}& =(\vec{\mathbf{a}}-{\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}})\cdot \vec{\mathbf{b}}\\ & =\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}-({\text{proj}}_{\vec{\mathbf{b}}}\vec{\mathbf{a}})\cdot \vec{\mathbf{b}}\\ & =\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}-\frac{(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})\vec{\mathbf{b}}}{b^2}\cdot \vec{\mathbf{b}}\\ & =\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}-\frac{(\vec{\mathbf{a}}\cdot \vec{\mathbf{b}})\cancel{b^2}}{\cancel{b^2}}=0\end{array}$$

Since $\vec{\mathbf{u}}\cdot \vec{\mathbf{b}}=0$ and neither $\vec{\mathbf{u}}$ nor $\vec{\mathbf{b}}$ themselves have a magnitude of zero, we must have that $\vec{\mathbf{u}}\perp \vec{\mathbf{b}}$.

Computing the Angle Between Vectors with Dot Products

From the definition $\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}=ab\cos \theta$ given at the beginning of the article, one can rearrange the formula to solve for $\theta ,$ the angle between the two vectors $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}.$

Angle Between Two Vectors

$$\theta =\arccos \left(\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{ab}\right)$$

This formula works for any two vectors $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ for which the dot product and magnitudes are known.

Practice Problem

Problem 1

Find the angle between the 2D vectors $\vec{\mathbf{a}}=⟨1,2⟩$ and $\vec{\mathbf{b}}=⟨3,4⟩.$

Solution 1

The angle can be found by means of the given formula and a calculator.

$$\begin{array}{rl}\theta & =\arccos \left(\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{ab}\right)\\ & =\arccos \left(\frac{a_x{b}_x+a_y{b}_y}{\sqrt{a_x^2+a_y^2}\sqrt{b_x^2+b_y^2}}\right)\\ & =\arccos \left(\frac{1\cdot 3+2\cdot 4}{\sqrt{1^2+2^2}\sqrt{3^2+4^2}}\right)\\ & \approx \boxed{10.3^{\circ }}\end{array}$$

Problem 2

Find the angle between the 3D vectors $\vec{\mathbf{a}}=⟨1,2,3⟩$ and $\vec{\mathbf{b}}=⟨4,5,6⟩.$

Solution 2

The angle can be found by means of the given formula and a calculator.

$$\begin{array}{rl}\theta & =\arccos \left(\frac{\vec{\mathbf{a}}\cdot \vec{\mathbf{b}}}{ab}\right)\\ & =\arccos \left(\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{\sqrt{a_x^2+a_y^2+a_z^2}\sqrt{b_x^2+b_y^2+b_z^2}}\right)\\ & =\arccos \left(\frac{1\cdot 4+2\cdot 5+3\cdot 6}{\sqrt{1^2+2^2+3^2}\sqrt{4^2+5^2+6^2}}\right)\\ & \approx \boxed{12.9^{\circ }}\end{array}$$